The Weibull distribution

Posted on by

Mathematically, the Weibull distribution has a simple definition. It is mathematically tractable. It is also a versatile model. The Weibull distribution is widely used in life data analysis, particularly in reliability engineering. In addition to analysis of fatigue data, the Weibull distribution can also be applied to other engineering problems, e.g. for modeling the so called weakest link model.This post gives an introduction to the Weibull distribution.

_______________________________________________________________________________________________

Defining the Weibull Distribution

A random variable Y is said to follow a Weibull distribution if Y has the following density function

    \displaystyle f(y)=\frac{\tau}{\lambda} \ \biggl( \frac{y}{\lambda} \biggr)^{\tau-1} \text{exp} \biggl[- \biggl(\frac{y}{\lambda}\biggr)^\tau \ \biggr] \ \ \ ;y>0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

where \tau>0 and \lambda>0 are some fixed constants. The notation \text{exp}[x] refers to the exponential function e^{x}. As defined here, the Weibull distribution is a two-parameter distribution with \tau being the shape parameter and \lambda being the scale parameter. The following is the cumulative distribution function (CDF).

    \displaystyle F(y)=1- \text{exp} \biggl[- \biggl(\frac{y}{\lambda}\biggr)^\tau \ \biggr] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)

_______________________________________________________________________________________________

Connection with the Exponential Distribution

The Weibull distribution can also arise naturally from the random sampling of an exponential random variable. A better way to view Weibull is through the lens of exponential. Taking an observation from an exponential distribution and raising it to a positive power will result in a Weibull observation. Specifically, the random variable \displaystyle Y=X^{\frac{1}{\tau}} has the same CDF as in (2) if X is an exponential random variable with mean \lambda^\tau. To see this, consider the following:

    \displaystyle \begin{aligned} P[Y \le y]&=P[X^{\frac{1}{\tau}} \le y] \\&=P[X \le y^{\tau}] \\&=1-e^{-\frac{y^{\tau}}{\lambda^\tau}} \\&=1-e^{-(\frac{y}{\lambda})^\tau} \end{aligned}

_______________________________________________________________________________________________

Basic Properties

The idea of the Weibull distribution as a power of an exponential distribution simplifies certain calculation on the Weibull distribution. For example, a raw moment of the Weibull distribution is simply another raw moment of the exponential distribution. For an exponential random variable X with mean \theta, the raw moments E[X^k] are (details can be found here):

    \displaystyle E[X^k]=\left\{ \begin{array}{ll} \displaystyle \Gamma(1+k) \ \theta^k &\ k>-1 \\ \text{ } & \text{ } \\ \displaystyle k! \ \theta^k &\ k \text{ is a positive integer} \end{array} \right.

where \Gamma(\cdot) is the gamma function. To see how the gamma function can be evaluated in Microsoft Excel, see the last section of this post.

For the Weibull random variable Y with parameters \tau and \lambda, i.e. Y=X^{1 / \tau} where X is the exponential random variable with mean \lambda^\tau, the following shows the mean and higher moments.

    \displaystyle E[Y]=E[X^{\frac{1}{\tau}}]=\Gamma \biggl(1+\frac{1}{\tau} \biggr) \ \lambda \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)

    \displaystyle E[Y^k]=E[X^{\frac{k}{\tau}}]=\Gamma \biggl(1+\frac{k}{\tau} \biggr) \ \lambda^k \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)

With the moments established, several other distributional quantities that are based on moments can also be established. The following shows the variance, skewness and kurtosis.

    \displaystyle Var[Y]=E[Y^2]-E[Y]^2=\biggl[ \Gamma \biggl(1+\frac{2}{\tau} \biggr)-\Gamma \biggl(1+\frac{1}{\tau} \biggr)^2 \biggr] \ \lambda^2 \ \ \ \ \ \ \ \ \ \ \ \ \ (5)

    \displaystyle \begin{aligned} \gamma_1&=\frac{E[(Y-\mu)^3}{\sigma^3} \\&=\frac{E[Y^3]-3 \ \mu \ E[Y^2]+2 \ \mu^3}{\sigma^3} \\&\displaystyle =\frac{\Gamma \biggl(1+\frac{3}{\tau} \biggr) \lambda^3-3 \ \mu \ \Gamma \biggl(1+\frac{2}{\tau} \biggr) \lambda^2+2 \ \mu^3}{(\sigma^2)^{\frac{3}{2}}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{aligned}

    \displaystyle \begin{aligned} \gamma_2&=\frac{E[(Y-\mu)^4}{\sigma^4} \\&=\frac{E[Y^4]-4 \ \mu \ E[Y^3]+6 \ \mu^2 \ E[Y^2]-3 \ \mu^4}{\sigma^4} \\&\displaystyle =\frac{\Gamma \biggl(1+\frac{4}{\tau} \biggr) \lambda^4-4 \ \mu \ \Gamma \biggl(1+\frac{3}{\tau} \biggr) \lambda^3+6 \ \mu^2 \ \Gamma \biggl(1+\frac{2}{\tau} \biggr) \lambda^2-3 \ \mu^4}{\sigma^4} \ \ \ \ \ (7) \end{aligned}

The notation \gamma_1 here is the skewness. The notation \gamma_2 is kurtosis. The excess kurtosis is \gamma_2-3. In some sources, the notation \gamma_2 is to denote excess kurtosis. Of course \mu and \sigma^2 are the mean and variance, respectively.

Another calculation that is easily accessible for the Weibull distribution is that of the percentiles. It is easy to solve for y in the CDF in (2). For example, to find the median, set the CDF equals to 0.5 and solves for y, producing the following.

    \displaystyle \text{median}=\lambda \ \biggl(\text{ln}(2) \biggr)^{\frac{1}{\tau}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8)

Another basic and important property to examine is the failure rate. The failure rate of a distribution is the ratio of the density function to its survival function. The following is the failure of the Weibull distribution.

    \displaystyle \mu(t)=\frac{f(t)}{1-F(t)}=\frac{\tau}{\lambda} \ \biggl( \frac{t}{\lambda} \biggr)^{\tau-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9)

See here for a discussion of the failure rate in conjunction with the exponential distribution. Suppose that the distribution in question is a lifetime distribution (time until termination or death). Then the failure rate \mu(t) can be interpreted as the rate of failure at the next instant given that the life has survived to time t.

_______________________________________________________________________________________________

When the Parameters Vary

The discussion in the previous section might give the impression that all Weibull distributions (when the parameters vary) behave in the same way. We now look at examples showing that as \tau (shape parameter) and/or \lambda (scale parameter) vary, the distribution will exhibit markedly different behavior. Note that when \tau=1, the Weibull distribution is reduced to the exponential distribution.

Example 1
The following diagram shows the PDFs of the Weibull distribution with \tau=0.5, \tau=1 and \tau=2 where \lambda=1 in all three cases.

Figure 1

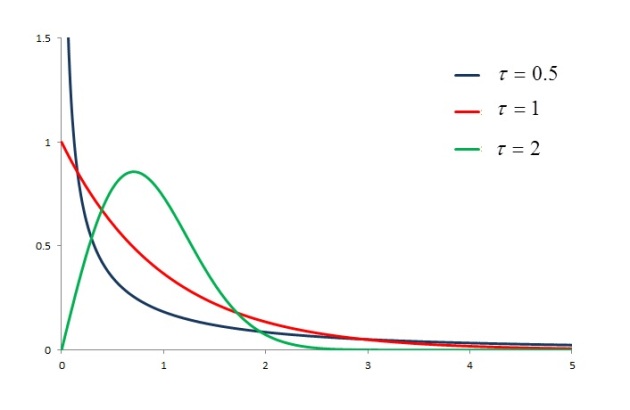
weibull-pdfs-2

Figure 1 shows the effect of the shape parameter taking on different values while keeping the scale parameter fixed. The effect is very pronounced on the skewness. All three density curves are right skewed. The PDF with \tau=0.5 (the blue curve) has a very strong right skew. The PDF with \tau=1 (the red curve) is exponential and has, by comparison, a much smaller skewness. The PDF with \tau=2 looks almost symmetric, though there is a clear and small right skew. This observation is borne out by the calculation. The skewness coefficients are \gamma_1=6.62 (blue curve), \gamma_1=2 (red curve) and \gamma_1=0.6311 (green curve).

Another clear effect of the shape parameter is the thickness of the tail (in this case the right tail). Figure 1 suggests that the PDF with \tau=0.5 (the blue curve) is higher than the other two density curves on the interval x>2. As a result, the blue curve has more probability mass in the right tail. Thus the blue curve has a thicker tail comparing to the other two PDFs. For a numerical confirmation, the following table compares the probabilities in the right tail.

    \displaystyle \begin{array}{lllllll} \text{ } &\text{ } & \tau=0.5 & \text{ } & \tau=1 & \text{ } & \tau=2 \\ \text{ } & \text{ } &\text{Blue Curve} & \text{ } & \text{Red Curve} & \text{ }& \text{Green Curve} \\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>2] &\text{ } & 0.2431 & \text{ } & 0.1353 & \text{ } & 0.0183\\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>3] &\text{ } & 0.1769 & \text{ } & 0.0498 & \text{ } & 0.0003355 \\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>4] &\text{ } & 0.1353 & \text{ } & 0.0183 & \text{ } & \displaystyle 1.125 \times 10^{-7} \\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>5] &\text{ } & 0.1069 & \text{ } & 0.00674 & \text{ } & 1.389 \times 10^{-11} \\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>10] &\text{ } & 0.0423 & \text{ } & 0.0000454 & \text{ } & 3.72 \times 10^{-44} \\ \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ P[X>25] &\text{ } & 0.00673 & \text{ } & 1.39 \times 10^{-11} & \text{ } & 3.68 \times 10^{-272} \end{array}

It is clear from the above table that the Weibull distribution with the blue curve assigns more probabilities to the higher values. The mean of the distribution for blue curve is 2. The right tail x>10 (over 5 times the mean) contains 4.23% of the probability mass (a small probability for sure but not negligible). The right tail x>25 (over 12.5 times the mean) still has a small probability of 0.00673 that cannot be totally ignored. On the other hand, the Weibull distribution for the green curve has a light tail. The mean of the distribution for the green curve is about 0.89. At x>4 (over 4.5 times of its mean), the tail probability is already negligible at 1.125 \times 10^{-7}. At x>10 (over 11 times of its mean), the tail probability is 3.72 \times 10^{-44}, practically zero.

Let’s compare the density curves in Figure 1 with their failure rates. The following figure shows the failure rates for these three Weibull distributions.

Figure 2

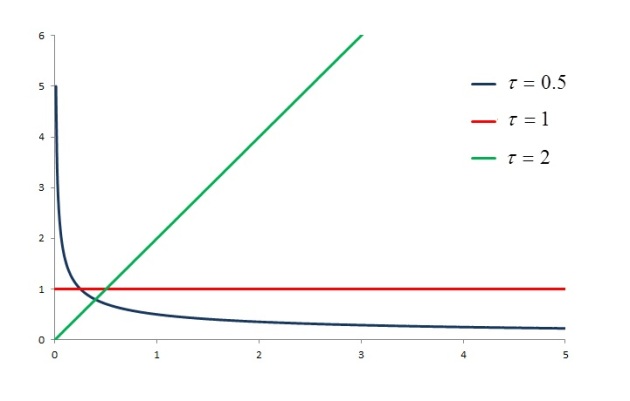
weibull-failure-rates

According to the definition in (9), the following shows the failure rate function for the three Weibull distributions.

    \mu(y)=\frac{0.5}{y^{0.5}} \ \ \ \ \ y>0 \ \ \ \ \ \ \ \tau=0.5 \ \ \text{(blue curve)}

    \mu(y)=1 \ \ \ \ \ \ \ \ y>0 \ \ \ \ \ \ \ \tau=1 \ \ \text{(red curve)}

    \mu(y)=2y \ \ \ \ \ \ y>0 \ \ \ \ \ \ \ \tau=2 \ \ \text{(green curve)}

The blue curve in Figure 1 (\tau=0.5) has a decreasing failure rate as shown in Figure 2. The failure rate function is constant for the case of \tau=1 (the exponential case). It is an increasing function for the case of \tau=2. This comparison shows that the Weibull distribution is particularly useful for engineers and researchers who study the reliability of machines and devices. If the engineers believe that the failure rate is constant, then an exponential model is appropriate. If they believe that the failure rate increases with time or age, then a Weibull distribution with shape parameter \tau>1 is more appropriate. If the engineers believe that the failure rate decreases with time, then a Weibull distribution with shape parameter \tau<1 is more appropriate.

Example 2
We now compare Weibull distributions with various values for \lambda (scale parameter) while keeping the shape parameter \tau fixed. The following shows the density curves for the Weibull distributions with \lambda=1, 2, 3 while keeping \tau=2.

Figure 3

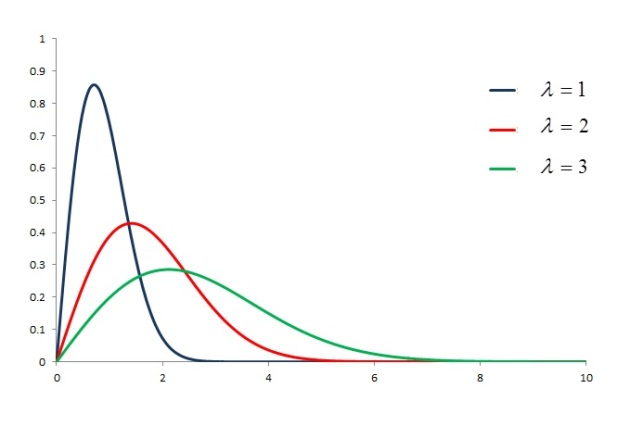
weibull-pdfs-3

The effect of the scale parameter \lambda is to compress or stretch out the standard Weibull density curve, i.e. the Weibull distribution with \lambda=1. For example, the density function for \lambda=2 is obtained by stretching out the density curve for the one with \lambda=1. The same overall shape is maintained while the density curve is being stretched or compressed. According to (3), the mean of the transformed distribution is increased (stretching) or decreased (compressing). For example, as \lambda is increased from 1 to 2, the mean has a two-fold increase. As the density curve is stretched, the resulting distribution is more spread out and the peak of the density curve decreases. The overall effect of changing the scale parameter is essentially a change in the scale in the x-axis.

The next example is a computational exercise.

Example 3
The time until failure (in months) of a semiconductor device has a Weibull distribution with shape parameter \tau=2.2 and scale parameter \lambda=400.

  • Give the density function and the survival function.
  • Determine the probability that the device will last at least 500 hours.
  • Determine the probability that the device will last at least 600 hours given that it has been running for over 500 hours.
  • Find the mean and standard deviation of the time until failure.
  • Determine the failure rate function of the Weibull time until failure.

To obtain the density function, the survival function and the failure rate, follow the relationships in (1), (2) and (9).

    \displaystyle f(y)=\frac{2.2}{400} \ \biggl( \frac{y}{400} \biggr)^{1.2} \text{exp} \biggl[- \biggl(\frac{y}{400}\biggr)^{2.2} \ \biggr]

    \displaystyle S(y)=\text{exp} \biggl[- \biggl(\frac{y}{400}\biggr)^{2.2} \biggr]

    \displaystyle \mu(y)=\frac{2.2}{400} \ \biggl( \frac{y}{400} \biggr)^{1.2}

Note that the Weibull failure rate is the ratio of the density function to the survival function. In this case, the failure is an increasing function of y. Since Y is a time scale, then this is a model for machines that wear out over time (see the next section).

The probability that the device will last over 500 hours is e^{-(\frac{500}{400})^{2.2}}=0.1952. The unconditional probability that the device will last over 600 hours is e^{-(\frac{600}{400})^{2.2}}=0.0872 The conditional probability that the device will last more than 600 hours given that it has lasted more 500 hours is the ratio \frac{S(600)}{S(500)}=0.4465.

To find the mean and variance, we need to evaluate the gamma function. Using Excel, we obtain the following two values of the gamma function (as shown here):

    \Gamma(1+\frac{1}{2.2})=0.88562476

    \Gamma(1+\frac{2}{2.2})=0.964912489

The mean and standard deviation of the time until failure are:

    E[Y]=\Gamma(1+\frac{1}{2.2}) \times 400=354.2499042

    E[Y^2]=\Gamma(1+\frac{2}{2.2}) \times 400^2=154385.9982

    Var[Y]=E[Y^2]-E[Y]^2=28893.00363

    \sigma_Y=\sqrt{Var[Y]}=169.9794212

_______________________________________________________________________________________________

The Weibull Failure Rates

Looking at the failure rate function indicated in (9) and looking at Figure 2, it is clear that when the shape parameter 0<\tau<1, the failure rate decreases with time (if the distribution is a model for the time until death of a life). When the shape parameter \tau=1, the failure rate is constant. When the shape parameter \tau>1, the failure rate increases with time. As a result, the Weibull family of distribution has a great deal of flexibility for modeling the failures of objects (machines, devices).

When the shape parameter 0<\tau<1, the failure rate decreases with time. Such a Weibull distribution is a model for infant mortality, or early-life failures. When the shape parameter \tau=1 (or near 1), the failure rate is constant or near constant. The resulting Weibull distribution (an exponential model) is a model for random failures (failures that are independent of age). When the shape parameter \tau>1, the failure rate increases with time. The resulting Weibull distribution is a model for wear-out failures.

In some applications, it may be necessary to model each phase of a lifetime separately, e.g. the early phase with a Weibull distribution with 0<\tau<1, the useful phase with a Weibull distribution with \tau close to 1 and the wear-out phase with a Weibull distribution with \tau>1. The resulting failure rate curve resembles a bathtub curve. The following is an idealized bathtub curve.

Figure 4

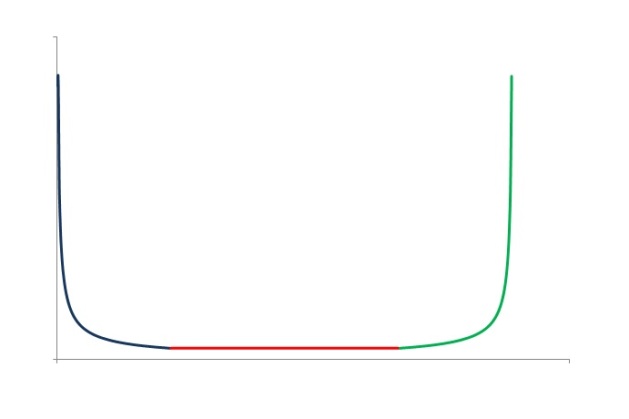
weibull-bathtub-failure-curve

The blue part of the bathtub curve is the early phase of the lifetime, which is characterized by decreasing failure rate. This is the early-life period in which the defective products die off and are taken out of the study. The next period is the useful-life period, the red part of the curve, in which the failures are random that are independent of age. In this phase, the failure rate is constant or near constant. The green part of the bathtub curve is characterized by increasing failure rates, which is the wear-out phase of the lifetime being studied.

_______________________________________________________________________________________________

Weakest Link Model

Another attractiveness of the Weibull model is that it can be used to model the so called the weakest link model. Consider a machine or device that has multiple components. Suppose that the device dies or fails when any one of the components fails. The lifetime of such a machine or device is the time to the first failure. Such a lifetime model is called the weakest link model. It can be shown that under these conditions a Weibull distribution is a good model for the distribution of the lifetime of such a machine or device.

If the time until failure of the individual components are indpendent and identically distributed Weibull random variables, then it follows that the minimum of of the Weibull random variables is also a Weibull random variable. To see this, let X_1,X_2,\cdots,X_n be independent and identically distributed Weibull random varaibles. Let \tau and \lambda be the parameters for the common Weibull distribution. Let Y=\text{min}(X_1,X_2,\cdots,X_n). The following gives the survival function of Y.

    \displaystyle \begin{aligned} P[Y >y]&=P[\text{all } X_i >y] \\&=\biggl(e^{-(\frac{y}{\lambda})^\tau} \biggr)^n \\&=e^{-n (\frac{y}{\lambda})^\tau} \\&=e^{-(\frac{y}{\lambda_1})^\tau} \end{aligned}

where \lambda_1=\frac{\lambda}{t} and t=n^{\frac{1}{\tau}}. This shows that Y has a Weibull distribution with shape parameter \tau (as before) and scale parameter \lambda_1. Under the condition that the times to failure for the multiple components are indentically Weibull distributed, the lifetime of the device is also a Weibull model.

_______________________________________________________________________________________________

The Moment Generating Function

The post is concluded with a comment on the moment generating function for the Weibull distribution. Note that relationship (4) indicates that all positive moments for the Weibull distribution exist. A natural question is on whether the moment generating function (MGF) exists. It turns out that MGF does not always exist for the Weibull distribution. The MGF exists for the Weibull distribution whenever the shape parameter \tau \ge 1. However the MGF cannot be expressed in terms of any familiar functions. Instead, the Weibull MGF can be expressed as a power series.

    \displaystyle M(t)=\sum \limits_{n=0}^\infty \ \frac{(\lambda t)^n}{n!} \ \Gamma \biggl(1+\frac{n}{\tau} \biggr) \ \ \ \ \ \tau \ge 1

To see this, start with the power series for e^x.

    \displaystyle e^X=\sum \limits_{n=0}^\infty \ \frac{X^n}{n!}

    \displaystyle e^{t X}=\sum \limits_{n=0}^\infty \ \frac{(t X)^n}{n!}

    \displaystyle M(t)=E[e^{t X}]=\sum \limits_{n=0}^\infty \ \frac{t^n}{n!} \ E[X^n]

    \displaystyle M(t)=\sum \limits_{n=0}^\infty \ \frac{(\lambda t)^n}{n!} \ \Gamma \biggl(1+\frac{n}{\tau} \biggr)

Since the positive moments exist for the Weibull distribution, the higher moments from (4) are plugged into the power series. It can be shown that the last series converges when \tau \ge 1.

When 0<\tau<1, the power series does not converge. For a specific example, let \tau=0.5. Then the term in the series is simplified to 2 \lambda t (2n+1), when goes to infinity when n \rightarrow \infty. Thus the Weilbull distribution with the shape parameter \tau=0.5 is an example of a distribution where all the positive moments exist but the MGF does not exist.

_______________________________________________________________________________________________

Further Information

Further information can be found here and here.

_______________________________________________________________________________________________
\copyright \ 2016 - \text{Dan Ma}